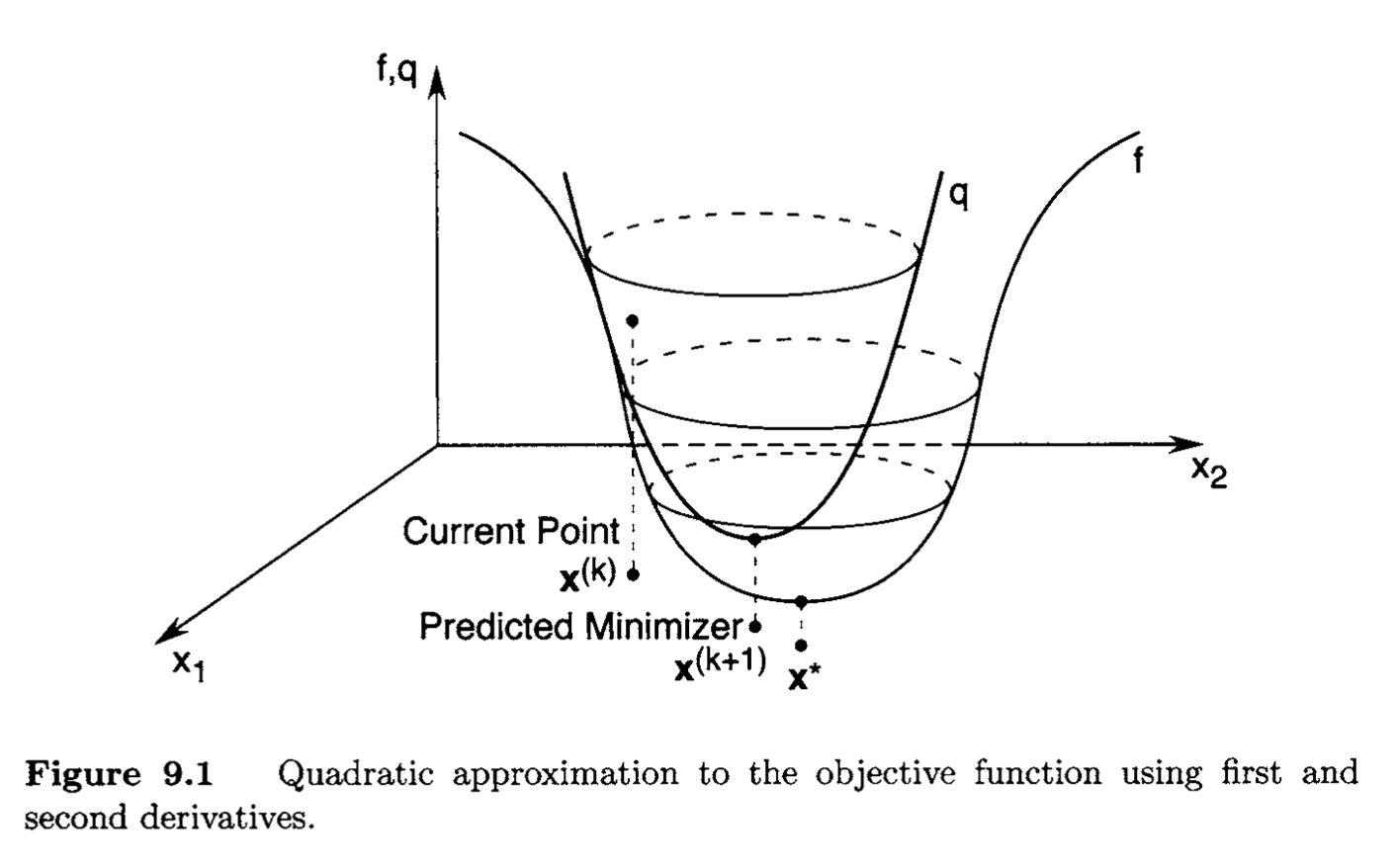
Multi-Dimensional Newton's Method Recall the one-dimensional Newton's Method presented in One-Dimensional Search Methods . Similarly, in a multi-dimensional setting, we minimize the approximate (quadratic) function that approaches to the value of the minimizer of the original function, illustrated in Figure 9.1.
We can obtain a quadratic approximation to the twice continuously differentiable objection function f : R n → R f:\mathbb{R}^n\to\mathbb{R} f : R n → R f f f x ( k ) x^{(k)} x ( k )
f ( x ) ≈ f ( x ( k ) ) + ( x − x ( k ) ) T g ( k ) + 1 2 ( x − x ( k ) ) T F ( x ( k ) ) ( x − x ( k ) ) ≜ q ( x ) , \begin{gather*} f(x) \approx f(x^{(k)})+(x-x^{(k)})^Tg^{(k)}+{1\over2}(x-x^{(k)})^TF(x^{(k)})(x-x^{(k)}) \triangleq q(x), \end{gather*} f ( x ) ≈ f ( x ( k ) ) + ( x − x ( k ) ) T g ( k ) + 2 1 ( x − x ( k ) ) T F ( x ( k ) ) ( x − x ( k ) ) ≜ q ( x ) , where, for simplicity, we use the notation g ( k ) = ∇ f ( x ( k ) ) g^{(k)}=\nabla f(x^{(k)}) g ( k ) = ∇ f ( x ( k ) ) q q q
0 = ∇ q ( x ) = g ( k ) + F ( x ( k ) ) ( x − x ( k ) ) . \begin{gather*} 0=\nabla q(x)=g^{(k)}+F(x^{(k)})(x-x^{(k)}). \end{gather*} 0 = ∇ q ( x ) = g ( k ) + F ( x ( k ) ) ( x − x ( k ) ) . if F ( x ( k ) ) > 0 F(x^{(k)})>0 F ( x ( k ) ) > 0 q q q
x ( k + 1 ) = x ( k ) − F ( x ( k ) ) − 1 g ( k ) . \begin{gather*} x^{(k+1)}=x^{(k)}-F(x^{(k)})^{-1}g^{(k)}. \end{gather*} x ( k + 1 ) = x ( k ) − F ( x ( k ) ) − 1 g ( k ) . This recursive formula represents Newton's method.
Quasi-Newton Methods A computational drawback of Newton's method is the need to evaluate F ( x ( k ) ) \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right) F ( x ( k ) ) F ( x ( k ) ) d ( k ) = − g ( k ) \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right) \boldsymbol{d}^{(k)}=-\boldsymbol{g}^{(k)} F ( x ( k ) ) d ( k ) = − g ( k ) d ( k ) = − F ( x ( k ) ) − 1 g ( k ) \boldsymbol{d}^{(k)}= -\boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right)^{-1} \boldsymbol{g}^{(k)} d ( k ) = − F ( x ( k ) ) − 1 g ( k ) F ( x ( k ) ) − 1 \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right)^{-1} F ( x ( k ) ) − 1 F ( x ( k ) ) − 1 \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right)^{-1} F ( x ( k ) ) − 1 F ( x ( k ) ) − 1 \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right)^{-1} F ( x ( k ) ) − 1 F ( x ( k ) ) − 1 \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right)^{-1} F ( x ( k ) ) − 1
x ( k + 1 ) = x ( k ) − α H k g ( k ) , \boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-\alpha \boldsymbol{H}_k \boldsymbol{g}^{(k)}, x ( k + 1 ) = x ( k ) − α H k g ( k ) , where H k \boldsymbol{H}_k H k n × n n \times n n × n α \alpha α f f f x ( k ) \boldsymbol{x}^{(k)} x ( k )
f ( x ( k + 1 ) ) = f ( x ( k ) ) + g ( k ) ⊤ ( x ( k + 1 ) − x ( k ) ) + o ( ∥ x ( k + 1 ) − x ( k ) ∥ ) = f ( x ( k ) ) − α g ( k ) ⊤ H k g ( k ) + o ( ∥ H k g ( k ) ∥ α ) . \begin{aligned} f\left(\boldsymbol{x}^{(k+1)}\right) &=f\left(\boldsymbol{x}^{(k)}\right)+\boldsymbol{g}^{(k) \top}\left(\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}\right)+o\left(\left\|\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}\right\|\right) \\ &=f\left(\boldsymbol{x}^{(k)}\right)-\alpha \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \boldsymbol{g}^{(k)}+o\left(\left\|\boldsymbol{H}_k \boldsymbol{g}^{(k)}\right\| \alpha\right) . \end{aligned} f ( x ( k + 1 ) ) = f ( x ( k ) ) + g ( k ) ⊤ ( x ( k + 1 ) − x ( k ) ) + o ( ∥ ∥ x ( k + 1 ) − x ( k ) ∥ ∥ ) = f ( x ( k ) ) − α g ( k ) ⊤ H k g ( k ) + o ( ∥ ∥ H k g ( k ) ∥ ∥ α ) . As α \alpha α f f f α \alpha α
g ( k ) ⊤ H k g ( k ) > 0. \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \boldsymbol{g}^{(k)}>0 . g ( k ) ⊤ H k g ( k ) > 0. A simple way to ensure this is to require that H k \boldsymbol{H}_k H k
Proposition Let f ∈ C 1 , x ( k ) ∈ R n , g ( k ) = ∇ f ( x ( k ) ) ≠ 0 f \in \mathcal{C}^1, \boldsymbol{x}^{(k)} \in \mathbb{R}^n, g^{(k)}=\nabla f\left(\boldsymbol{x}^{(k)}\right) \neq 0 f ∈ C 1 , x ( k ) ∈ R n , g ( k ) = ∇ f ( x ( k ) ) = 0 H k \boldsymbol{H}_k H k n × n n \times n n × n x ( k + 1 ) = \boldsymbol{x}^{(k+1)}= x ( k + 1 ) = x ( k ) − α k H k g ( k ) \boldsymbol{x}^{(k)}-\alpha_k \boldsymbol{H}_k \boldsymbol{g}^{(k)} x ( k ) − α k H k g ( k ) α k = arg min α ≥ 0 f ( x ( k ) − α H k g ( k ) ) \alpha_k=\arg \min _{\alpha \geq 0} f\left(\boldsymbol{x}^{(k)}-\alpha \boldsymbol{H}_k \boldsymbol{g}^{(k)}\right) α k = arg min α ≥ 0 f ( x ( k ) − α H k g ( k ) ) α k > 0 \alpha_k>0 α k > 0 f ( x ( k + 1 ) ) < f ( x ( k ) ) f\left(\boldsymbol{x}^{(k+1)}\right)<f\left(\boldsymbol{x}^{(k)}\right) f ( x ( k + 1 ) ) < f ( x ( k ) )
In constructing an approximation to the inverse of the Hessian matrix, we should use only the objective function and gradient values. Thus, if we can find a suitable method of choosing H k \boldsymbol{H}_k H k
Approximating the Inverse Hessian Let H 0 , H 1 , H 2 , … \boldsymbol{H}_0, \boldsymbol{H}_1, \boldsymbol{H}_2, \ldots H 0 , H 1 , H 2 , … F ( x ( k ) ) − 1 \boldsymbol{F}\left(\boldsymbol{x}^{(k)}\right)^{-1} F ( x ( k ) ) − 1 F ( x ) \boldsymbol{F}(\boldsymbol{x}) F ( x ) f f f x \boldsymbol{x} x F ( x ) = Q \boldsymbol{F}(\boldsymbol{x})=\boldsymbol{Q} F ( x ) = Q x \boldsymbol{x} x Q = Q ⊤ \boldsymbol{Q}=\boldsymbol{Q}^{\top} Q = Q ⊤
g ( k + 1 ) − g ( k ) = Q ( x ( k + 1 ) − x ( k ) ) \boldsymbol{g}^{(k+1)}-\boldsymbol{g}^{(k)}=\boldsymbol{Q}\left(\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}\right) g ( k + 1 ) − g ( k ) = Q ( x ( k + 1 ) − x ( k ) ) Let
Δ g ( k ) ≜ g ( k + 1 ) − g ( k ) \Delta \boldsymbol{g}^{(k)} \triangleq \boldsymbol{g}^{(k+1)}-\boldsymbol{g}^{(k)} Δ g ( k ) ≜ g ( k + 1 ) − g ( k ) and then, we may write
Δ x ( k ) ≜ x ( k + 1 ) − x ( k ) . \Delta \boldsymbol{x}^{(k)} \triangleq \boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)} . Δ x ( k ) ≜ x ( k + 1 ) − x ( k ) . We start with a real symmetric positive definite matrix H 0 \boldsymbol{H}_0 H 0 k k k Q − 1 \boldsymbol{Q}^{-1} Q − 1
Q − 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k . \boldsymbol{Q}^{-1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, \quad 0 \leq i \leq k . Q − 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k . Therefore, we also impose the requirement that the approximation H k + 1 \boldsymbol{H}_{k+1} H k + 1
H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k . \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, \quad 0 \leq i \leq k . H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k . If n n n n n n Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) \Delta \boldsymbol{x}^{(0)}, \Delta \boldsymbol{x}^{(1)}, \ldots, \Delta \boldsymbol{x}^{(n-1)} Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 )
H n Δ g ( 0 ) = Δ x ( 0 ) , H n Δ g ( 1 ) = Δ x ( 1 ) , ⋮ H n Δ g ( n − 1 ) = Δ x ( n − 1 ) . \begin{aligned} \boldsymbol{H}_n \Delta \boldsymbol{g}^{(0)} &=\Delta \boldsymbol{x}^{(0)}, \\ \boldsymbol{H}_n \Delta \boldsymbol{g}^{(1)} &=\Delta \boldsymbol{x}^{(1)}, \\ & \vdots \\ \boldsymbol{H}_n \Delta \boldsymbol{g}^{(n-1)} &=\Delta \boldsymbol{x}^{(n-1)} . \end{aligned} H n Δ g ( 0 ) H n Δ g ( 1 ) H n Δ g ( n − 1 ) = Δ x ( 0 ) , = Δ x ( 1 ) , ⋮ = Δ x ( n − 1 ) . This set of equations can be represented as
H n [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] = [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] \boldsymbol{H}_n\left[\Delta \boldsymbol{g}^{(0)}, \Delta \boldsymbol{g}^{(1)}, \ldots, \Delta \boldsymbol{g}^{(n-1)}\right]=\left[\Delta \boldsymbol{x}^{(0)}, \Delta \boldsymbol{x}^{(1)}, \ldots, \Delta \boldsymbol{x}^{(n-1)}\right] H n [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] = [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] Note that Q Q Q
Q [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] = [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] \boldsymbol{Q}\left[\Delta \boldsymbol{x}^{(0)}, \Delta \boldsymbol{x}^{(1)}, \ldots, \Delta \boldsymbol{x}^{(n-1)}\right]=\left[\Delta \boldsymbol{g}^{(0)}, \Delta \boldsymbol{g}^{(1)}, \ldots, \Delta \boldsymbol{g}^{(n-1)}\right] Q [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] = [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] and
Q − 1 [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] = [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] \boldsymbol{Q}^{-1}\left[\Delta \boldsymbol{g}^{(0)}, \Delta \boldsymbol{g}^{(1)}, \ldots, \Delta \boldsymbol{g}^{(n-1)}\right]=\left[\Delta \boldsymbol{x}^{(0)}, \Delta \boldsymbol{x}^{(1)}, \ldots, \Delta \boldsymbol{x}^{(n-1)}\right] Q − 1 [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] = [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] Therefore, if [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] \left[\Delta g^{(0)}, \Delta g^{(1)}, \ldots, \Delta g^{(n-1)}\right] [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] Q − 1 Q^{-1} Q − 1 n n n
Q − 1 = H n = [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] − 1 \boldsymbol{Q}^{-1}=\boldsymbol{H}_n=\left[\Delta \boldsymbol{x}^{(0)}, \Delta \boldsymbol{x}^{(1)}, \ldots, \Delta \boldsymbol{x}^{(n-1)}\right]\left[\Delta \boldsymbol{g}^{(0)}, \Delta \boldsymbol{g}^{(1)}, \ldots, \Delta \boldsymbol{g}^{(n-1)}\right]^{-1} Q − 1 = H n = [ Δ x ( 0 ) , Δ x ( 1 ) , … , Δ x ( n − 1 ) ] [ Δ g ( 0 ) , Δ g ( 1 ) , … , Δ g ( n − 1 ) ] − 1 As a consequence, we conclude that if H n \boldsymbol{H}_n H n H n Δ g ( i ) = \boldsymbol{H}_n \Delta \boldsymbol{g}^{(i)}= H n Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ n − 1 \Delta \boldsymbol{x}^{(i)}, 0 \leq i \leq n-1 Δ x ( i ) , 0 ≤ i ≤ n − 1 x ( k + 1 ) = x ( k ) − α k H k g ( k ) \boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-\alpha_k \boldsymbol{H}_k \boldsymbol{g}^{(k)} x ( k + 1 ) = x ( k ) − α k H k g ( k ) α k = arg min α ≥ 0 f ( x ( k ) − α H k g ( k ) ) \alpha_k=\arg \min _{\alpha \geq 0} f\left(\boldsymbol{x}^{(k)}-\alpha \boldsymbol{H}_k \boldsymbol{g}^{(k)}\right) α k = arg min α ≥ 0 f ( x ( k ) − α H k g ( k ) ) n + 1 n+1 n + 1 x ( n + 1 ) = \boldsymbol{x}^{(n+1)}= x ( n + 1 ) = x ( n ) − α n H n g ( n ) \boldsymbol{x}^{(n)}-\alpha_n \boldsymbol{H}_n \boldsymbol{g}^{(n)} x ( n ) − α n H n g ( n ) n n n n n n
The considerations above illustrate the basic idea behind the quasi-Newton methods. Specifically, quasi-Newton algorithms have the form
d ( k ) = − H k g ( k ) α k = arg min α ≥ 0 f ( x ( k ) + α d ( k ) ) x ( k + 1 ) = x ( k ) + α k d ( k ) \begin{aligned} \boldsymbol{d}^{(k)} &=-\boldsymbol{H}_k \boldsymbol{g}^{(k)} \\ \alpha_k &=\underset{\alpha \geq 0}{\arg \min } f\left(\boldsymbol{x}^{(k)}+\alpha \boldsymbol{d}^{(k)}\right) \\ \boldsymbol{x}^{(k+1)} &=\boldsymbol{x}^{(k)}+\alpha_k \boldsymbol{d}^{(k)} \end{aligned} d ( k ) α k x ( k + 1 ) = − H k g ( k ) = α ≥ 0 arg min f ( x ( k ) + α d ( k ) ) = x ( k ) + α k d ( k ) where the matrices H 0 , H 1 , … \boldsymbol{H}_0, \boldsymbol{H}_1, \ldots H 0 , H 1 , …
H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k , \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, \quad 0 \leq i \leq k, H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k , where Δ x ( i ) = x ( i + 1 ) − x ( i ) = α i d ( i ) \Delta \boldsymbol{x}^{(i)}=\boldsymbol{x}^{(i+1)}-\boldsymbol{x}^{(i)}=\alpha_i \boldsymbol{d}^{(i)} Δ x ( i ) = x ( i + 1 ) − x ( i ) = α i d ( i ) Δ g ( i ) = g ( i + 1 ) − g ( i ) = Q Δ x ( i ) \Delta \boldsymbol{g}^{(i)}=\boldsymbol{g}^{(i+1)}-\boldsymbol{g}^{(i)}=\boldsymbol{Q} \Delta \boldsymbol{x}^{(i)} Δ g ( i ) = g ( i + 1 ) − g ( i ) = Q Δ x ( i )
Theorem Consider a quasi-Newton algorithm applied to a quadratic function with Hessian Q = Q ⊤ \boldsymbol{Q}=\boldsymbol{Q}^{\top} Q = Q ⊤ 0 ≤ k < n − 1 0 \leq k<n-1 0 ≤ k < n − 1
H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k , \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, \quad 0 \leq i \leq k, H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k , where H k + 1 = H k + 1 ⊤ \boldsymbol{H}_{k+1}=\boldsymbol{H}_{k+1}^{\top} H k + 1 = H k + 1 ⊤ α i ≠ 0 , 0 ≤ i ≤ k \alpha_i \neq 0,0 \leq i \leq k α i = 0 , 0 ≤ i ≤ k d ( 0 ) , … , d ( k + 1 ) \boldsymbol{d}^{(0)}, \ldots, \boldsymbol{d}^{(k+1)} d ( 0 ) , … , d ( k + 1 ) Q \boldsymbol{Q} Q
Proof We proceed by induction. We begin with the k = 0 k=0 k = 0 d ( 0 ) \boldsymbol{d}^{(0)} d ( 0 ) d ( 1 ) \boldsymbol{d}^{(1)} d ( 1 ) Q \boldsymbol{Q} Q α 0 ≠ 0 \alpha_0 \neq 0 α 0 = 0 d ( 0 ) = Δ x ( 0 ) / α 0 \boldsymbol{d}^{(0)}=\Delta \boldsymbol{x}^{(0)} / \alpha_0 d ( 0 ) = Δ x ( 0 ) / α 0
d ( 1 ) ⊤ Q d ( 0 ) = − g ( 1 ) ⊤ H 1 Q d ( 0 ) = − g ( 1 ) ⊤ H 1 Q Δ x ( 0 ) α 0 = − g ( 1 ) ⊤ H 1 Δ g ( 0 ) α 0 = − g ( 1 ) ⊤ Δ x ( 0 ) α 0 = − g ( 1 ) ⊤ d ( 0 ) \begin{aligned} \boldsymbol{d}^{(1) \top} \boldsymbol{Q} \boldsymbol{d}^{(0)} &=-\boldsymbol{g}^{(1) \top} \boldsymbol{H}_1 \boldsymbol{Q} \boldsymbol{d}^{(0)} \\ &=-\boldsymbol{g}^{(1) \top} \boldsymbol{H}_1 \frac{\boldsymbol{Q} \Delta \boldsymbol{x}^{(0)}}{\alpha_0} \\ &=-\boldsymbol{g}^{(1) \top} \frac{\boldsymbol{H}_1 \Delta \boldsymbol{g}^{(0)}}{\alpha_0} \\ &=-\boldsymbol{g}^{(1) \top} \frac{\Delta \boldsymbol{x}^{(0)}}{\alpha_0} \\ &=-\boldsymbol{g}^{(1) \top} \boldsymbol{d}^{(0)} \end{aligned} d ( 1 ) ⊤ Q d ( 0 ) = − g ( 1 ) ⊤ H 1 Q d ( 0 ) = − g ( 1 ) ⊤ H 1 α 0 Q Δ x ( 0 ) = − g ( 1 ) ⊤ α 0 H 1 Δ g ( 0 ) = − g ( 1 ) ⊤ α 0 Δ x ( 0 ) = − g ( 1 ) ⊤ d ( 0 ) But g ( 1 ) ⊤ d ( 0 ) = 0 \boldsymbol{g}^{(1) \top} \boldsymbol{d}^{(0)}=0 g ( 1 ) ⊤ d ( 0 ) = 0 α 0 > 0 \alpha_0>0 α 0 > 0 ϕ ( α ) = \phi(\alpha)= ϕ ( α ) = f ( x ( 0 ) + α d ( 0 ) ) f\left(\boldsymbol{x}^{(0)}+\alpha \boldsymbol{d}^{(0)}\right) f ( x ( 0 ) + α d ( 0 ) ) d ( 1 ) ⊤ Q d ( 0 ) = 0 \boldsymbol{d}^{(1) \top} \boldsymbol{Q} \boldsymbol{d}^{(0)}=0 d ( 1 ) ⊤ Q d ( 0 ) = 0
Assume that the result is true for k − 1 k-1 k − 1 k < n − 1 k<n-1 k < n − 1 k k k d ( 0 ) , … , d ( k + 1 ) \boldsymbol{d}^{(0)}, \ldots, \boldsymbol{d}^{(k+1)} d ( 0 ) , … , d ( k + 1 ) Q \boldsymbol{Q} Q d ( k + 1 ) ⊤ Q d ( i ) = 0 , 0 ≤ i ≤ k \boldsymbol{d}^{(k+1) \top} \boldsymbol{Q} \boldsymbol{d}^{(i)}=0,0 \leq i \leq k d ( k + 1 ) ⊤ Q d ( i ) = 0 , 0 ≤ i ≤ k i , 0 ≤ i ≤ k i, 0 \leq i \leq k i , 0 ≤ i ≤ k k = 0 k=0 k = 0 α i ≠ 0 \alpha_i \neq 0 α i = 0
d ( k + 1 ) ⊤ Q d ( i ) = − g ( k + 1 ) ⊤ H k + 1 Q d ( i ) ⋮ = − g ( k + 1 ) ⊤ d ( i ) \begin{aligned} \boldsymbol{d}^{(k+1) \top} \boldsymbol{Q} \boldsymbol{d}^{(i)} &=-\boldsymbol{g}^{(k+1) \top} \boldsymbol{H}_{k+1} \boldsymbol{Q} \boldsymbol{d}^{(i)} \\ & \vdots \\ &=-\boldsymbol{g}^{(k+1) \top} \boldsymbol{d}^{(i)} \end{aligned} d ( k + 1 ) ⊤ Q d ( i ) = − g ( k + 1 ) ⊤ H k + 1 Q d ( i ) ⋮ = − g ( k + 1 ) ⊤ d ( i ) Because d ( 0 ) , … , d ( k ) \boldsymbol{d}^{(0)}, \ldots, \boldsymbol{d}^{(k)} d ( 0 ) , … , d ( k ) Q \boldsymbol{Q} Q 10.2 10.2 10.2 g ( k + 1 ) ⊤ d ( i ) = 0 \boldsymbol{g}^{(k+1)^{\top}} \boldsymbol{d}^{(i)}=0 g ( k + 1 ) ⊤ d ( i ) = 0 d ( k + 1 ) ⊤ Q d ( i ) = 0 \boldsymbol{d}^{(k+1)^{\top}} \boldsymbol{Q} \boldsymbol{d}^{(i)}=0 d ( k + 1 ) ⊤ Q d ( i ) = 0
By this theorem, we conclude that a quasi-Newton algorithm solves a quadratic of n n n n n n
Note that the equations that the matrices H k \boldsymbol{H}_k H k H k \boldsymbol{H}_k H k H k + 1 \boldsymbol{H}_{k+1} H k + 1 H k \boldsymbol{H}_k H k
In the rank one correction formula, the correction term is symmetric and has the form a k z ( k ) z ( k ) ⊤ a_k \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top} a k z ( k ) z ( k ) ⊤ a k ∈ R a_k \in \mathbb{R} a k ∈ R z ( k ) ∈ R n \boldsymbol{z}^{(k)} \in \mathbb{R}^n z ( k ) ∈ R n
H k + 1 = H k + a k z ( k ) z ( k ) ⊤ . \boldsymbol{H}_{k+1}=\boldsymbol{H}_k+a_k \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top} . H k + 1 = H k + a k z ( k ) z ( k ) ⊤ . Note that
rank z ( k ) z ( k ) ⊤ = rank ( [ z 1 ( k ) ⋮ z n ( k ) ] [ z 1 ( k ) ⋯ z n ( k ) ] ) = 1 \operatorname{rank} \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top}=\operatorname{rank}\left(\left[\begin{array}{c} z_1^{(k)} \\ \vdots \\ z_n^{(k)} \end{array}\right]\left[\begin{array}{lll} z_1^{(k)} & \cdots & z_n^{(k)} \end{array}\right]\right)=1 rank z ( k ) z ( k ) ⊤ = rank ⎝ ⎛ ⎣ ⎡ z 1 ( k ) ⋮ z n ( k ) ⎦ ⎤ [ z 1 ( k ) ⋯ z n ( k ) ] ⎠ ⎞ = 1 and hence the name rank one correction [it is also called the single-rank symmetric (SRS) algorithm]. The product z ( k ) z ( k ) ⊤ \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top} z ( k ) z ( k ) ⊤ H k \boldsymbol{H}_k H k H k + 1 \boldsymbol{H}_{k+1} H k + 1
Our goal now is to determine a k a_k a k z ( k ) \boldsymbol{z}^{(k)} z ( k ) H k , Δ g ( k ) , Δ x ( k ) \boldsymbol{H}_k, \Delta \boldsymbol{g}^{(k)}, \Delta \boldsymbol{x}^{(k)} H k , Δ g ( k ) , Δ x ( k )
H k + 1 Δ g ( i ) = Δ x ( i ) , i = 1 , … , k \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, i=1, \ldots, k H k + 1 Δ g ( i ) = Δ x ( i ) , i = 1 , … , k H k + 1 Δ g ( k ) = Δ x ( k ) \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(k)}=\Delta \boldsymbol{x}^{(k)} H k + 1 Δ g ( k ) = Δ x ( k ) H k , Δ g ( k ) \boldsymbol{H}_k, \Delta \boldsymbol{g}^{(k)} H k , Δ g ( k ) Δ x ( k ) \Delta \boldsymbol{x}^{(k)} Δ x ( k ) a k a_k a k z ( k ) \boldsymbol{z}^{(k)} z ( k )
H k + 1 Δ g ( k ) = ( H k + a k z ( k ) z ( k ) ⊤ ) Δ g ( k ) = Δ x ( k ) . \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(k)}=\left(\boldsymbol{H}_k+a_k \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top}\right) \Delta \boldsymbol{g}^{(k)}=\Delta \boldsymbol{x}^{(k)} . H k + 1 Δ g ( k ) = ( H k + a k z ( k ) z ( k ) ⊤ ) Δ g ( k ) = Δ x ( k ) . First note that z ( k ) ⊤ Δ g ( k ) \boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)} z ( k ) ⊤ Δ g ( k )
Δ x ( k ) − H k Δ g ( k ) = ( a k z ( k ) ⊤ Δ g ( k ) ) z ( k ) , \Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}=\left(a_k \boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)}\right) \boldsymbol{z}^{(k)}, Δ x ( k ) − H k Δ g ( k ) = ( a k z ( k ) ⊤ Δ g ( k ) ) z ( k ) , and hence
z ( k ) = Δ x ( k ) − H k Δ g ( k ) a k ( z ( k ) ⊤ Δ g ( k ) ) . \boldsymbol{z}^{(k)}=\frac{\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}}{a_k\left(\boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)}\right)} . z ( k ) = a k ( z ( k ) ⊤ Δ g ( k ) ) Δ x ( k ) − H k Δ g ( k ) . We can now determine
a k z ( k ) z ( k ) ⊤ = ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ a k ( z ( k ) ⊤ Δ g ( k ) ) 2 . a_k \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top}=\frac{\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top}}{a_k\left(\boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)}\right)^2} . a k z ( k ) z ( k ) ⊤ = a k ( z ( k ) ⊤ Δ g ( k ) ) 2 ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ . Hence,
H k + 1 = H k + ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ a k ( z ( k ) ⊤ Δ g ( k ) ) 2 . \boldsymbol{H}_{k+1}=\boldsymbol{H}_k+\frac{\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top}}{a_k\left(\boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)}\right)^2} . H k + 1 = H k + a k ( z ( k ) ⊤ Δ g ( k ) ) 2 ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ . The next step is to express the denominator of the second term on the righthand side of the equation above as a function of the given quantities H k \boldsymbol{H}_k H k Δ g ( k ) \Delta \boldsymbol{g}^{(k)} Δ g ( k ) Δ x ( k ) \Delta \boldsymbol{x}^{(k)} Δ x ( k ) Δ x ( k ) − H k Δ g ( k ) = \Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}= Δ x ( k ) − H k Δ g ( k ) = ( a k z ( k ) ⊤ Δ g ( k ) ) z ( k ) \left(a_k \boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)}\right) \boldsymbol{z}^{(k)} ( a k z ( k ) ⊤ Δ g ( k ) ) z ( k ) Δ g ( k ) ⊤ \Delta \boldsymbol{g}^{(k) \top} Δ g ( k ) ⊤
Δ g ( k ) ⊤ Δ x ( k ) − Δ g ( k ) ⊤ H k Δ g ( k ) = Δ g ( k ) ⊤ a k z ( k ) z ( k ) ⊤ Δ g ( k ) \Delta \boldsymbol{g}^{(k) \top} \Delta \boldsymbol{x}^{(k)}-\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}=\Delta \boldsymbol{g}^{(k) \top} a_k \boldsymbol{z}^{(k)} \boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)} Δ g ( k ) ⊤ Δ x ( k ) − Δ g ( k ) ⊤ H k Δ g ( k ) = Δ g ( k ) ⊤ a k z ( k ) z ( k ) ⊤ Δ g ( k ) Observe that a k a_k a k Δ g ( k ) ⊤ z ( k ) = z ( k ) ⊤ Δ g ( k ) \Delta \boldsymbol{g}^{(k) \top} \boldsymbol{z}^{(k)}=\boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)} Δ g ( k ) ⊤ z ( k ) = z ( k ) ⊤ Δ g ( k )
Δ g ( k ) ⊤ Δ x ( k ) − Δ g ( k ) ⊤ H k Δ g ( k ) = a k ( z ( k ) ⊤ Δ g ( k ) ) 2 \Delta \boldsymbol{g}^{(k) \top} \Delta \boldsymbol{x}^{(k)}-\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}=a_k\left(\boldsymbol{z}^{(k) \top} \Delta \boldsymbol{g}^{(k)}\right)^2 Δ g ( k ) ⊤ Δ x ( k ) − Δ g ( k ) ⊤ H k Δ g ( k ) = a k ( z ( k ) ⊤ Δ g ( k ) ) 2 Taking this relation into account yields
H k + 1 = H k + ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( k ) ⊤ ( Δ x ( k ) − H k Δ g ( k ) ) . \boldsymbol{H}_{k+1}=\boldsymbol{H}_k+\frac{\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top}}{\Delta \boldsymbol{g}^{(k) \top}\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)} . H k + 1 = H k + Δ g ( k ) ⊤ ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ . We summarize the above development in the following algorithm.
Rank One Algorithm Set k : = 0 k:=0 k := 0 x ( 0 ) \boldsymbol{x}^{(0)} x ( 0 ) H 0 \boldsymbol{H}_0 H 0 If g ( k ) = 0 \boldsymbol{g}^{(k)}=\mathbf{0} g ( k ) = 0 d ( k ) = − H k g ( k ) \boldsymbol{d}^{(k)}=-\boldsymbol{H}_k \boldsymbol{g}^{(k)} d ( k ) = − H k g ( k ) Computeα k = arg min α ≥ 0 f ( x ( k ) + α d ( k ) ) = − g ( k ) T d ( k ) d ( k ) T Q d ( k ) when f is quadratic, x ( k + 1 ) = x ( k ) + α k d ( k ) \begin{aligned} \alpha_k &=\underset{\alpha \geq 0}{\arg \min } f\left(\boldsymbol{x}^{(k)}+\alpha \boldsymbol{d}^{(k)}\right) \\ &=-{\boldsymbol{g}^{(k)T}\boldsymbol{d}^{(k)}\over \boldsymbol{d}^{(k)T}\boldsymbol{Q}\boldsymbol{d}^{(k)}}\text{ when $f$ is quadratic, } \\ \boldsymbol{x}^{(k+1)} &=\boldsymbol{x}^{(k)}+\alpha_k \boldsymbol{d}^{(k)} \end{aligned} α k x ( k + 1 ) = α ≥ 0 arg min f ( x ( k ) + α d ( k ) ) = − d ( k ) T Q d ( k ) g ( k ) T d ( k ) when f is quadratic, = x ( k ) + α k d ( k ) ComputeΔ x ( k ) = α k d ( k ) Δ g ( k ) = g ( k + 1 ) − g ( k ) , H k + 1 = H k + ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( k ) ⊤ ( Δ x ( k ) − H k Δ g ( k ) ) \begin{aligned} &\Delta \boldsymbol{x}^{(k)}=\alpha_k \boldsymbol{d}^{(k)} \\ &\Delta \boldsymbol{g}^{(k)}=\boldsymbol{g}^{(k+1)}-\boldsymbol{g}^{(k)}, \\ &\boldsymbol{H}_{k+1}=\boldsymbol{H}_k+\frac{\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top}}{\Delta \boldsymbol{g}^{(k) \top}\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)} \end{aligned} Δ x ( k ) = α k d ( k ) Δ g ( k ) = g ( k + 1 ) − g ( k ) , H k + 1 = H k + Δ g ( k ) ⊤ ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Set k : = k + 1 k:=k+1 k := k + 1 H k + 1 Δ g ( k ) = Δ x ( k ) . \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(k)}=\Delta \boldsymbol{x}^{(k)} . H k + 1 Δ g ( k ) = Δ x ( k ) . H k + 1 Δ g ( i ) = Δ x ( i ) , i = 0 , 1 , … , k . \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, \quad i=0,1, \ldots, k . H k + 1 Δ g ( i ) = Δ x ( i ) , i = 0 , 1 , … , k . Theorem For the rank one algorithm applied to the quadratic with Hessian Q = Q ⊤ \operatorname{sian} \boldsymbol{Q}=\boldsymbol{Q}^{\top} sian Q = Q ⊤ H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, 0 \leq i \leq k H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k
Proof We prove the result by induction. From the discussion before the theorem, it is clear that the claim is true for k = 0 k=0 k = 0 k − 1 ≥ 0 k-1 \geq 0 k − 1 ≥ 0 H k Δ g ( i ) = Δ x ( i ) , i < k \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, i<k H k Δ g ( i ) = Δ x ( i ) , i < k k k k
H k + 1 Δ g ( k ) = Δ x ( k ) . \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(k)}=\Delta \boldsymbol{x}^{(k)} . H k + 1 Δ g ( k ) = Δ x ( k ) . So we only have to show that
H k + 1 Δ g ( i ) = Δ x ( i ) , i < k . \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, \quad i<k . H k + 1 Δ g ( i ) = Δ x ( i ) , i < k . To this end, fix i < k i<k i < k
H k + 1 Δ g ( i ) = H k Δ g ( i ) + ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( k ) ⊤ ( Δ x ( k ) − H k Δ g ( k ) ) Δ g ( i ) \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}+\frac{\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top}}{\Delta \boldsymbol{g}^{(k) \top}\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)} \Delta \boldsymbol{g}^{(i)} H k + 1 Δ g ( i ) = H k Δ g ( i ) + Δ g ( k ) ⊤ ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( i ) By the induction hypothesis, H k Δ g ( i ) = Δ x ( i ) \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)} H k Δ g ( i ) = Δ x ( i )
( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( i ) = Δ x ( k ) ⊤ Δ g ( i ) − Δ g ( k ) ⊤ H k Δ g ( i ) = 0 \left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(i)}-\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}=0 ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( i ) = Δ x ( k ) ⊤ Δ g ( i ) − Δ g ( k ) ⊤ H k Δ g ( i ) = 0 Indeed, since
Δ g ( k ) ⊤ H k Δ g ( i ) = Δ g ( k ) ⊤ ( H k Δ g ( i ) ) = Δ g ( k ) ⊤ Δ x ( i ) \Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{g}^{(k) \top}\left(\boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}\right)=\Delta \boldsymbol{g}^{(k) \top} \Delta \boldsymbol{x}^{(i)} Δ g ( k ) ⊤ H k Δ g ( i ) = Δ g ( k ) ⊤ ( H k Δ g ( i ) ) = Δ g ( k ) ⊤ Δ x ( i ) by the induction hypothesis, and because Δ g ( k ) = Q Δ x ( k ) \Delta g^{(k)}=Q \Delta x^{(k)} Δ g ( k ) = Q Δ x ( k )
Δ g ( k ) ⊤ H k Δ g ( i ) = Δ g ( k ) ⊤ Δ x ( i ) = Δ x ( k ) ⊤ Q Δ x ( i ) = Δ x ( k ) ⊤ Δ g ( i ) . \Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{g}^{(k) \top} \Delta \boldsymbol{x}^{(i)}=\Delta \boldsymbol{x}^{(k) \top} \boldsymbol{Q} \Delta \boldsymbol{x}^{(i)}=\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(i)} . Δ g ( k ) ⊤ H k Δ g ( i ) = Δ g ( k ) ⊤ Δ x ( i ) = Δ x ( k ) ⊤ Q Δ x ( i ) = Δ x ( k ) ⊤ Δ g ( i ) . Hence,
( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( i ) = Δ x ( k ) ⊤ Δ g ( i ) − Δ x ( k ) ⊤ Δ g ( i ) = 0 \left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right)^{\top} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(i)}-\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(i)}=0 ( Δ x ( k ) − H k Δ g ( k ) ) ⊤ Δ g ( i ) = Δ x ( k ) ⊤ Δ g ( i ) − Δ x ( k ) ⊤ Δ g ( i ) = 0 which completes the proof.
The DFP Algorithm (Rank Two Update) Set k : = 0 k:=0 k := 0 x ( 0 ) \boldsymbol{x}^{(0)} x ( 0 ) H 0 \boldsymbol{H}_0 H 0 If g ( k ) = 0 \boldsymbol{g}^{(k)}=\mathbf{0} g ( k ) = 0 d ( k ) = − H k g ( k ) \boldsymbol{d}^{(k)}=-\boldsymbol{H}_k \boldsymbol{g}^{(k)} d ( k ) = − H k g ( k ) Computeα k = arg min α ≥ 0 f ( x ( k ) + α d ( k ) ) , x ( k + 1 ) = x ( k ) + α k d ( k ) . \begin{aligned} \alpha_k &=\underset{\alpha \geq 0}{\arg \min } f\left(\boldsymbol{x}^{(k)}+\alpha \boldsymbol{d}^{(k)}\right), \\ \boldsymbol{x}^{(k+1)} &=\boldsymbol{x}^{(k)}+\alpha_k \boldsymbol{d}^{(k)} . \end{aligned} α k x ( k + 1 ) = α ≥ 0 arg min f ( x ( k ) + α d ( k ) ) , = x ( k ) + α k d ( k ) . ComputeΔ x ( k ) = α k d ( k ) , Δ g ( k ) = g ( k + 1 ) − g ( k ) , H k + 1 = H k + Δ x ( k ) Δ x ( k ) ⊤ Δ x ( k ) ⊤ Δ g ( k ) − [ H k Δ g ( k ) ] [ H k Δ g ( k ) ] ⊤ Δ g ( k ) ⊤ H k Δ g ( k ) . \begin{aligned} \Delta \boldsymbol{x}^{(k)} &=\alpha_k \boldsymbol{d}^{(k)}, \\ \Delta \boldsymbol{g}^{(k)} &=\boldsymbol{g}^{(k+1)}-\boldsymbol{g}^{(k)}, \\ \boldsymbol{H}_{k+1} &=\boldsymbol{H}_k+\frac{\Delta \boldsymbol{x}^{(k)} \Delta \boldsymbol{x}^{(k) \top}}{\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(k)}}-\frac{\left[\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right]\left[\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}\right]^{\top}}{\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}} . \end{aligned} Δ x ( k ) Δ g ( k ) H k + 1 = α k d ( k ) , = g ( k + 1 ) − g ( k ) , = H k + Δ x ( k ) ⊤ Δ g ( k ) Δ x ( k ) Δ x ( k ) ⊤ − Δ g ( k ) ⊤ H k Δ g ( k ) [ H k Δ g ( k ) ] [ H k Δ g ( k ) ] ⊤ . Set k : = k + 1 k:=k+1 k := k + 1 H k + 1 Δ g ( i ) ≐ Δ x ( i ) \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)} \doteq \Delta \boldsymbol{x}^{(i)} H k + 1 Δ g ( i ) ≐ Δ x ( i ) 0 ≤ i ≤ k 0 \leq i \leq k 0 ≤ i ≤ k Theorem In the DFP algorithm applied to the quadratic with Hessian Q = Q ⊤ \boldsymbol{Q}=\boldsymbol{Q}^{\top} Q = Q ⊤ H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, 0 \leq i \leq k H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k k = 0 k=0 k = 0
H 1 Δ g ( 0 ) = H 0 Δ g ( 0 ) + Δ x ( 0 ) Δ x ( 0 ) ⊤ Δ x ( 0 ) ⊤ Δ g ( 0 ) Δ g ( 0 ) − H 0 Δ g ( 0 ) Δ g ( 0 ) ⊤ H 0 Δ g ( 0 ) ⊤ H 0 Δ g ( 0 ) Δ g ( 0 ) = Δ x ( 0 ) \begin{aligned} \boldsymbol{H}_1 \Delta \boldsymbol{g}^{(0)} &=\boldsymbol{H}_0 \Delta \boldsymbol{g}^{(0)}+\frac{\Delta \boldsymbol{x}^{(0)} \Delta \boldsymbol{x}^{(0) \top}}{\Delta \boldsymbol{x}^{(0) \top} \Delta \boldsymbol{g}^{(0)}} \Delta \boldsymbol{g}^{(0)}-\frac{\boldsymbol{H}_0 \Delta \boldsymbol{g}^{(0)} \Delta \boldsymbol{g}^{(0) \top} \boldsymbol{H}_0}{\Delta \boldsymbol{g}^{(0) \top} \boldsymbol{H}_0 \Delta \boldsymbol{g}^{(0)}} \Delta \boldsymbol{g}^{(0)} \\ &=\Delta \boldsymbol{x}^{(0)} \end{aligned} H 1 Δ g ( 0 ) = H 0 Δ g ( 0 ) + Δ x ( 0 ) ⊤ Δ g ( 0 ) Δ x ( 0 ) Δ x ( 0 ) ⊤ Δ g ( 0 ) − Δ g ( 0 ) ⊤ H 0 Δ g ( 0 ) H 0 Δ g ( 0 ) Δ g ( 0 ) ⊤ H 0 Δ g ( 0 ) = Δ x ( 0 ) Assume that the result is true for k − 1 k-1 k − 1 H k Δ g ( i ) = Δ x ( i ) , 0 ≤ \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, 0 \leq H k Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k − 1 i \leq k-1 i ≤ k − 1 H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)}, 0 \leq i \leq k H k + 1 Δ g ( i ) = Δ x ( i ) , 0 ≤ i ≤ k i = k i=k i = k
H k + 1 Δ g ( k ) = H k Δ g ( k ) + Δ x ( k ) Δ x ( k ) ⊤ Δ x ( k ) ⊤ Δ g ( k ) Δ g ( k ) − H k Δ g ( k ) Δ g ( k ) ⊤ H k Δ g ( k ) ⊤ H k Δ g ( k ) Δ g ( k ) = Δ x ( k ) \begin{aligned} \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(k)} &=\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}+\frac{\Delta \boldsymbol{x}^{(k)} \Delta \boldsymbol{x}^{(k) \top}}{\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(k)}} \Delta \boldsymbol{g}^{(k)}-\frac{\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)} \Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k}{\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}} \Delta \boldsymbol{g}^{(k)} \\ &=\Delta \boldsymbol{x}^{(k)} \end{aligned} H k + 1 Δ g ( k ) = H k Δ g ( k ) + Δ x ( k ) ⊤ Δ g ( k ) Δ x ( k ) Δ x ( k ) ⊤ Δ g ( k ) − Δ g ( k ) ⊤ H k Δ g ( k ) H k Δ g ( k ) Δ g ( k ) ⊤ H k Δ g ( k ) = Δ x ( k ) It remains to consider the case i < k i<k i < k
H k + 1 Δ g ( i ) = H k Δ g ( i ) + Δ x ( k ) Δ x ( k ) ⊤ Δ x ( k ) ⊤ Δ g ( k ) Δ g ( i ) − H k Δ g ( k ) Δ g ( k ) ⊤ H k Δ g ( k ) ⊤ H k Δ g ( k ) Δ g ( i ) = Δ x ( i ) + Δ x ( k ) Δ x ( k ) ⊤ Δ g ( k ) ( Δ x ( k ) ⊤ Δ g ( i ) ) − H k Δ g ( k ) Δ g ( k ) ⊤ H k Δ g ( k ) ( Δ g ( k ) ⊤ Δ x ( i ) ) \begin{aligned} \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=& \boldsymbol{H}_k \Delta \boldsymbol{g}^{(i)}+\frac{\Delta \boldsymbol{x}^{(k)} \Delta \boldsymbol{x}^{(k) \top}}{\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(k)}} \Delta \boldsymbol{g}^{(i)}-\frac{\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)} \Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k}{\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}} \Delta \boldsymbol{g}^{(i)} \\ =& \Delta \boldsymbol{x}^{(i)}+\frac{\Delta \boldsymbol{x}^{(k)}}{\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(k)}}\left(\Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(i)}\right) \\ &-\frac{\boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}}{\Delta \boldsymbol{g}^{(k) \top} \boldsymbol{H}_k \Delta \boldsymbol{g}^{(k)}}\left(\Delta \boldsymbol{g}^{(k) \top} \Delta \boldsymbol{x}^{(i)}\right) \end{aligned} H k + 1 Δ g ( i ) = = H k Δ g ( i ) + Δ x ( k ) ⊤ Δ g ( k ) Δ x ( k ) Δ x ( k ) ⊤ Δ g ( i ) − Δ g ( k ) ⊤ H k Δ g ( k ) H k Δ g ( k ) Δ g ( k ) ⊤ H k Δ g ( i ) Δ x ( i ) + Δ x ( k ) ⊤ Δ g ( k ) Δ x ( k ) ( Δ x ( k ) ⊤ Δ g ( i ) ) − Δ g ( k ) ⊤ H k Δ g ( k ) H k Δ g ( k ) ( Δ g ( k ) ⊤ Δ x ( i ) ) Now,
Δ x ( k ) ⊤ Δ g ( i ) = Δ x ( k ) ⊤ Q Δ x ( i ) = α k α i d ( k ) ⊤ Q d ( i ) = 0 , \begin{aligned} \Delta \boldsymbol{x}^{(k) \top} \Delta \boldsymbol{g}^{(i)} &=\Delta \boldsymbol{x}^{(k) \top} \boldsymbol{Q} \Delta \boldsymbol{x}^{(i)} \\ &=\alpha_k \alpha_i \boldsymbol{d}^{(k) \top} \boldsymbol{Q} \boldsymbol{d}^{(i)} \\ &=0, \end{aligned} Δ x ( k ) ⊤ Δ g ( i ) = Δ x ( k ) ⊤ Q Δ x ( i ) = α k α i d ( k ) ⊤ Q d ( i ) = 0 , by the induction hypothesis and Theorem 11.1. The same arguments yield Δ g ( k ) ⊤ Δ x ( i ) = 0 \Delta \boldsymbol{g}^{(k) \top} \Delta \boldsymbol{x}^{(i)}=0 Δ g ( k ) ⊤ Δ x ( i ) = 0
H k + 1 Δ g ( i ) = Δ x ( i ) \boldsymbol{H}_{k+1} \Delta \boldsymbol{g}^{(i)}=\Delta \boldsymbol{x}^{(i)} H k + 1 Δ g ( i ) = Δ x ( i ) which completes the proof.
We conclude that the DFP algorithm is a conjugate direction algorithm.